Возврат к оглавлению книги.

As I have said, Einstein's theory stood outside the main stream of physical thought during the years between its inception and the end of the first world war. I return now to the more general historical account.

We left it at the point at which the conflict between Newtonian mechanics and Maxwell-Lorentz electromagnetism was at its sharpest, and the outstanding demonstration of this conflict was the Michelson-Morley experiment. This has been described a countless number of times, but never, so far as I know, *1 without the tacit introduction of an interpretation of the experiment that vitiates the deductions drawn from its results. The experiment, described in outline as far as possible without such an introduction, was simply this. A beam of light was split into two parts, which were sent, by means of mirrors, to and fro along two equal mutually perpendicular, material arms. On returning to their starting-point they interfered with one another, producing a pattern of dark and bright fringes of the kind familiar to students of optics. Consider the case in which one of the arms lay along the direction of the Earth's orbital motion around the Sun according to the universally accepted Copernican astronomical system assumed in Newtonian mechanics. At two times (instants), six months apart, that motion would be in opposite directions, so that, according to the Maxwell-Lorentz electromagnetic theory, in which the velocity of light was independent of the motion of its source, it is easily calculated that the fringes seen should be in different positions at the two instants. In fact, however, the fringes remained in the same position throughout the year.

Clearly something was wrong, and there were three possibilities concerning that something: (1) the Maxwell-Lorentz theory was wrong; (2) Newtonian mechanics was wrong; (3) there was some unknown effect of motion that had been neglected. But what was universally overlooked (apart from a later suggestion by Ritz, of which more presently) was that the first possibility was virtually excluded from consideration by the manner in which the experiment was described. It is practically always presented as a comparison of the times (durations) taken by the two beams of light to travel along their respective paths, and it is stated that these durations, which should have varied during the course of the year, kept constant throughout the year. But in fact no 'times' at all, of any kind, were measured. No clocks were used, so that no modification of 'time', however the word be construed so long as it is regarded as something related to clocks, could have anything to do with the result of the experiment. Before the experiment can be expressed in terms of 'times', the fringes observed must be interpreted in terms of the Maxwell-Lorentz electromagnetic theory, so that that theory is embedded in the very description of what has to be explained. Consequently, possibility (1) is quite illegitimately ruled out before we begin the explanation.

As we have seen, Einstein adopted possibility (2), which, though not proposed primarily for the purpose of explaining this experiment, was in fact applied to that purpose. But before that, possibility (3) - that there was some neglected effect of motion - had been suggested, first by FitzGerald and later independently by Lorentz; and here we meet another of those extraordinary oversights, of the same type as that by which Maxwell's theory is universally held to be at bottom identical with Faraday's although it is fundamentally different, which arise from the neglect of the study of the history of science, and the general practice by which erroneous statements, when once published, tend to be repeated perpetually by later writers.

The neglected effect of motion proposed by FitzGerald was a change in the dimensions of material bodies caused by their motion through the ether. Consider the case in which one arm of the apparatus (the longitudinal arm) lies in the direction of the Earth's orbital motion, while the other (the transverse arm) is at right angles to that direction. It is clear that if the length of one of those arms were changed by the motion while the other remained unchanged, a shift of the interference fringes would be expected to be caused thereby, for the distances travelled by the two beams of light would no longer be equal. If, however, this effect were equal and opposite to that expected to occur on account of the motion of the arms relative to the light, the absence of a fringe-shift would be accounted for. This is what FitzGerald proposed, on the basis of the electrical theory of matter which was very prominent at that time (the early 1890-s), and the suggestion is always known as the FitzGerald contraction. FitzGerald appears to have left no account of it, and we know it only through the report of it by Sir Oliver Lodge. The usual reference to this report is a brief indefinite mention in Nature, but a much fuller account — the most complete, I believe, that we have - is given in Lodge's book. The Ether of Space¹. Here he records that the suggestion was made verbally to him while they were discussing the problem in Lodge's study in Liverpool, and he gives the following account:

Lodge's account, it is true, does not make it perfectly clear whether this is his explanation of the effect or FitzGerald's, but since he leaves no doubt that the fundamental idea was FitzGerald's, it is unlikely that he would change it without saying so, and in that case there is no such thing as the 'FitzGerald contraction'; it is FitzGerald expasion, for, according to this explanation, it is not the longitudinal arm that is contracted but the transverse arm that is lengthened - the effect on the fringes, of course, being the same. To put the matter in a nutshell, an unelectrified rod at rest, according to the ideas of the time, consisted of equal quantities of positive and negative electricity in some form or other. When the rod was set in motion, these charges became two parallel currents of electricity in opposite directions, and such currents were known to repel one another. Accordingly, there was a force increasing the breadth of the longitudinal arm (which did not affect the path of the light) and the length of the transverse arm. Hence the FitzGerald effect was not a contraction of the former but an expansion of the latter.

However, independently of this and in ignorance of it, Lorentz in I904² proposed a much more comprehensive theory which, if valid, not only explained the null result of the Michelson-Morley experiment but provided a supplement to the Maxwell theory which implied that any experiment with material systems, carried out on bodies moving uniformly with respect to one another, would give exactly the same result, so that it would be inherently impossible to tell, from an experiment confined to a body, whether that body was at rest or moving uniformly through the ether. His proposal was that motion of a material body through the ether produced a contraction in the direction of motion, and a slowing down of all rhythmical processes, both by the factor (1 – v²/c²)^1/2, where v was the velocity of the body and c the velocity of light. Lorentz showed that if these physical effects were a reality, the relation between the co-ordinates, (x, t) of an event referred to one system, and the coordinates, (x', t'), of the same event referred to a system moving uniformly in the direction with respect to the first (for simplicity we consider one direction only - that of the relative motion - and suppose certain initial conditions to be satisfied) was given by the equations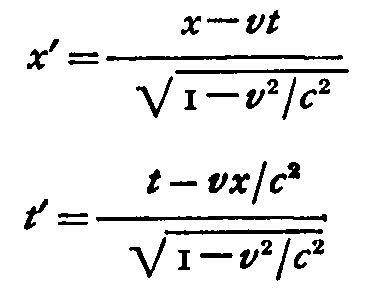

These equations are known as the Lorentz transformation. Mathematically their significance lies in the fact that, in mathematical language, the equations of the Maxwell-Lorcntz electromagnetic theory are invariant to them; that is to say, if, for x and t in those equations, we substitute the values given by the Lorentz transformation, we obtain identical equations with x', t' taking the places of x, t, and v changing to —v. This guaranteed that all measurements made on cither of two bodies, in uniform relative motion with velocity v (or —v), when interpreted in terms of the Maxwell-Lorentz theory, would be related in the same way, so that no physical observations confined to either of the bodies could distinguish the motion of that body from the motion of the other. It would still be possible, of course, by comparing observations on the two bodies, to detect effects of their relative motion, but experiments such as that of Michelson and Morley, for example, which were confined to the Earth, could not reveal the motion of the Earth.*2

This proposal became known as the relativity theory of Lorentz, and certain features of it call for attention here. In the first place, Lorentz recognised that it was a purely ad hoc hypothesis: it did not, like the more limited FitzGerald suggestion, give any explanation of the proposed physical effects. These were proposed simply because they led to a transformation to which the equations of the electromagnetic theory were invariant. 'It need hardly be said,' wrote Lorentz, 'that the present theory is put forward with all due reserve.' Nevertheless, it was a physical theory, not a mathematical one; that is to say, the proposal was that motion through the ether produced physical effects on bodies, and the mathematics expressed the physical results produced. Like Maxwell, who realised the necessity, if he was to satisfy his mathematical desires, of postulating a 'displacement current' to justify them, so Lorentz, in order to justify his transformation equations, saw the necessity of postulating a physical effect of interaction between moving matter and ether, to give the mathematics meaning. Physics still had de jure authority over mathematics: it was Einstein, who had no qualms about abolishing the ether and still retaining light waves whose properties were expressed by formulae that were meaningless without it, who was the first to discard physics altogether and propose a wholly mathematical theory.

Moreover, Lorentz entitled his paper, 'Electromagnetic Phenomena in a System moving with any Velocity less than that of Light' - thereby implying that, unlike the later theory of Einstein, his proposal did not prohibit velocities of systems greater than that of light. Again, there was no suggestion of any modification of Newtonian mechanics, of which it is certain Lorentz had no intention at all. But, in view of later events, perhaps the most serious aspect of the comparison of Lorentz's theory with Einstein's was the fact that both were called 'relativity' theories, for this, as we shall sec, has led to a confusion that I think has been the most effective agent in allowing Einstein's theory to persist so long in spite of its manifest impossibility. Strictly speaking, the name 'relativity theory' should be applied only to a theory that regards motion as a purely relative phenomenon — i.e. a theory that, like Einstein's, allows no ether. Lorentz's theory demanded an ether. He, and the great majority of his contemporaries, never doubted the physical reality of the ether, as something that both had physical properties and could serve as a standard of rest with respect to which 'absolute' velocities had a definite meaning.

But we shall not understand the position at all unless we realise that, from 1904 until the eclipse observations of 1919 that brought Einstein's general relativity theory to everyone's notice, 'the theory of relativity' meant, to almost all concerned, Lorentz's theory: Einstein's, if it was known at all, was regarded merely as a more obscure form of a theory that belonged to Lorentz. The name, 'Lorentz transformation', which is still used to denote the mathematical part of Einstein's theory, is a relic of that identification. Both Lorentz and Einstein, of course, knew the difference, but very few others did, or, for that matter, do now. The difference between that time and ours is that the earlier workers ascribed the supposedly single 'relativity' theory uniquely to Lorentz, and we to Einstein. Whittaker, in his History* partly restored to Lorentz the credit due to him, but even he made the mistake of identifying two quite different theories. As a pure mathematician he was naturally predisposed to label a theory by its mathematical rather than its physical content, and since that was the same for both theories, he credited it to the author of the earlier paper. He had, moreover, first-hand recollection of the circumstances of origin of the relevant papers. But Lorentz himself said, so late as 1928, 'the theory of relativity is really solely Einstein's work',⁴ and he was, of course, speaking at a time when the phrase 'the theory of relativity' had really come to mean to everyone a theory devised by Einstein - and, as Whittaker rightly points out, Lorentz did not accept it.

Ritz, who was alone in adopting what I have called (p. 161) possibility (1) of explaining the Michelson-Morley experiment, in a paper of more than a hundred pages published in 19085 criticising the existing electromagnetic theory, scarcely mentions Einstein; he is wholly concerned with Lorentz's justification of the theory, and no one reading it would imagine that Einstein had done anything at all in connection with the matter. Lodge, in the book already mentioned¹ (published in 1909), also does not mention Einstein; he regards Lorentz alone as the author of a complete system into which FitzGcrald's idea fitted. Poincare, in an address in 1912 published posthumously, says, during a discussion of a paper of Einstein's on the action of light on molecules: "nous n'avons qu'a appliquer le principe de relativite de Lorentz".⁶ It is inconceivable that he would have used such a phrase in such a connection had he regarded Einstein as having any claim at all to authorship of 'le principe de relativite'.

I think this will be enough to show how little Einstein was thought of in connection with the theory of relativity until his name became associated with it through his general theory. Born in Germany, Ritz in Switzerland, Poincare in France, the Cambridge physicists in England, More in America - all physicists concerned with this or closely related fields of work - failed to connect Einstein's name with it for years after his definitive paper had appeared. But one man - Minkowski, a mathematician, not a physicist, whose contribution, in view of its later outstanding influence compels notice here - had certainly heard of Einstein as well as Lorentz, though he, a mathematician, did not see how essentially distinct the two theories were, and Born, who attended his lectures on the subject, reports that he did not hear the name of Einstein mentioned in them. His distinctive feature, among the few to whose notice the work of both men had come, was that he regarded Einstein's presentation of the theory as the one to be preferred, and that precisely because he was a mathematician and not a physicist. He gave yet another form to the general complex of ideas which later became known as the special theory of relativity, and this must be given special notice here, not only because it provided Einstein with the type of mathematical machinery which he was to use in his later general theory, but also, and chiefly, because it contributed perhaps more than any other single factor to the transformation of mathematics from the servant into the master of physics, and introduced more false ideas into the subject - pre-eminently the totally irrelevant idea of time (eternity) - than anything else. It is to Minkowski that we owe the idea of a space-time' as an objective reality - which is perhaps the chief agent in the transformation of the whole subject from the ground of intelligible physics into the heaven (or hell) of metaphysics, where it has become, instead of an object for intelligent inquiry, an idol to be blindly worshipped.

That is to say, the process of allowing mathematics to direct physics, which began with Maxwell - albeit apologetically and with a recognition of the necessity for a physical justification for following the direction — had now reached a point at which it is taken as the proper function of mathematics to order physics along the path which mathematics points out, and mathematics is chided for neglecting this duty and allowing physics to choose its own way. The return to mediaeval scholasticism, against which the protest of Bacon and the other pioneers of modern science was thought to have been finally successful, was now complete. With Minkowski's work physics had escaped from experiment and been captured by mathematicians.

How could this happen? Mainly, I think, because, as we have seen, the ground had already been partly prepared for it, but also because Minkowski's work was then hardly known and quite unnoticed by physicists; its influence came much later when, as we shall see, it was made overwhelming by the reinforcement which it received from the mathematical form of Einstein's general theory. But just consider what Minkowski's work actually was. Remember that, according to his own assertion, he is writing as a mathematician, doing what mathematicians should have done before the physical considerations of Lorentz and Einstein had been conceived. He takes — quite arbitrarily, of course, in these circumstances — one of an infinite number of mathematical expressions (he might as well, of course, have taken, say, x — ty²/z or any other), and finds the transformation of symbols to which it is invariant. Mathematically the symbols are just symbols and nothing else. He then says, again entirely arbitrarily, 'Let x, y, z be rectangular co-ordinates for space, and let t denote time... The multiplicity of all thinkable x, y, z, t, systems of values we will christen the world.' Why? Why should not a mathematician ('fancy-free'!) equally well say, 'Let x denote pressure, y volume, z specific heat, and t temperature', then choose some combination of them, and announce laws of thermodynamics which would save the physicists the trouble of making observations? Of course, as anyone can see, Minkowski was entirely dependent on what was known or believed on physical grounds for his very choice of starting-point, yet he claims that what he did should have been done a priori with no physics at all. It is no wonder that Einstein's reasoning was a revelation to Max Born, who had become familiar, as he says, 'with the relativistic idea and the Lorentz transformations' through attending the lectures of Minkowski. Compared with Minkowski's approach, Einstein's, though much less physical than Lorentz's, was empirical in the extreme.

Minkowski brought the first to completion, but he was almost, if not quite, wholly responsible for the second. When he wrote 'Let x, y, z be rectangular co-ordinates for space, and let t denote time', he introduced something new and something wholly metaphysical into the subject. Never before in physics - not even in the theories of Lorentz and Einstein - had x, y, z denoted space or t time (eternity); they had meant respectively place and time (instant). In no application of any formula of physics, and in no co-ordinate diagram, does any co-ordinate have the significance of an indefinitely extended continuum, for the simple reason that all the formulae and diagrams represent relations between what can be observed, and space and time (eternity) cannot be observed. When we plot volume against pressure in a thermodynamic graph, no one dreams of the F-axis as representing space; it is simply a direction along which we mark off the measurable volume occupied by the material system we are considering; and the same restriction applies to pressure. Hence, when Minkowski let x, y, z represent space, and t, time (eternity), he was doing something quite unrelated to physics, and his famous conclusion, 'Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality', is utterly unwarranted: it is a conclusion about things not dealt with in physics, drawn from a purely gratuitous interpretation of an arbitrarily adopted mathematical formula. It is just as true or false or meaningless as an assertion that pressure and volume are shadows and only a kind of union of the two is real. The fact - if it be a fact - that the Lorentz transformation is physically significant simply means that, in the expression of the relation between our measurements when we refer them to different co-ordinate systems, the values of x, y, z, t are associated with one another and are not such that t always remains separate from the others. That no more means that space and time (in any sense) are arbitrary parts of a single absolute whole than the fact that pressure and volume do not change independently when the temperature is altered means that pressure and volume vanish to shadows, and only a union of the two has objective existence. It is impossible, I think, to form an adequate conception of the harm that this misrepresentation has caused, which quite overshadows whatever value Minkowski's mathematical representation of the mathematics of relativity theory has had in stimulating Einstein to the production of his general theory.

The immediate effect, such as it was, of Minkowski's paper was mainly one of mystification; Einstein himself is reported to have said that after reading it he felt he did not understand his own theory — which is not surprising, since Minkowski's 'time' was only 'eternity' and Einstein's was only 'instant' or 'duration'. Indeed, Einstein is often at pains to insist that 'time' means 'time of an event' and is denoted by the reading of a clock: what clock can read 'eternity'? Philipp Frank, in his Life of Einstein,¹⁰ tells us that Einstein, in his early days, attended Minkowski's lectures and was repelled by them, and Born, as we have seen, found Einstein's papers a 'revelation' after studying under Minkowski, though he never escaped from the influence of his early training, as I dunk his reply to my criticism (pp. 42-3) shows: he automatically interpreted 'time' as 'eternity', and assumed that that was what I, quoting Einstein, should have meant by it. 'The simple fact,' he wrote, that all relations between space co-ordinates and time expressed by the Lorentz transformation can be represented geometrically by Minkowski diagrams should suffice to show that there can be no logical contradiction in the theory.'¹¹ This is but one example of the endless confusion that has been introduced into the special relativity theory by the identification of the quite different meanings of the word 'time' (or 'Zeit') in the work of Einstein and Minkowski.

Of course, as is well known, Einstein later adopted the Minkowski form of his special theory as a basis for his general theory,¹² and superficially this may be regarded as an acceptance by Einstein of Minkowski's idea of 'space-time' as a physical reality. But the appearance is only superficial. In Einstein's general theory also, in so far as it can be applied to observation and receive support from it, the symbols x, y, z, t always refer to the places and instants of events, and the speculations - some of them very wild indeed - that have been advanced concerning the nature of 'space-time', 'the universe', and so on, are meaningless unless they can be translated into terms in which 'space' is potentially 'place' and 'time' is potentially 'instant'. If that can be done, such a term as 'space-time' may afford a convenient means of expression, just as one may speak of 'a considerable length of time' without implying that a duration can be measured with a yardstick, but in much modern cosmology, those who speak of 'space-time' naively imagine that it refers literally to something existing objectively, and so deceive themselves and others into thinking that the world which is the world of all of us has an esoteric quality that only the specially gifted can understand.

To resume the historical account, however, the important fact to grasp is that, from 1904 to the time of the first world war, the relativity theory so-called - which was a matter of interest only to a comparatively few, highly theoretical, physicists — was ascribed by all of them to Lorentz. The work of Einstein and Minkowski was little known, and those who were aware of it regarded it as simply more obscure forms of the generally intelligible and acceptable, though admittedly in need of experimental demonstration, theory of Lorentz. Tolman, indeed, many years later told me that when he first read Minkowski's paper his immediate reaction was, 'This is all hooey', and he tossed it aside without further attention. With his excess of modesty he related this as an example of his lack of insight, but I am inclined to give it the opposite interpretation so far as its relation to physics, as distinct from mathematics, is concerned. But Einstein, whose preoccupation after the completion of his special theory was with a generalisation of the relativity postulate to cover accelerated motion and so provide a theory of gravitation, possessed insight of a different kind. Quite understandably, he did not recognise the physical aspect of his own special theory in Minkowski's work, but he did recognise the possibilities of Minkowski's mathematics, when combined with the new tensor calculus of Ricci and Levi-Civita, for his desired generalisation, and step by step he approached the complete general theory which he published in 1916, in which a theory of gravitation was advanced that satisfied the relativity postulate (i.e. it regarded all motion, of whatever kind, as purely relative, so that if two bodies were in any kind of relative motion, the motion could be divided between them equally legitimately in whatever way one chose).

Before proceeding with our main theme - the explanation of the acceptance of Einstein's special theory notwithstanding its obvious impossibility — a word should be said concerning the relation of that to his general theory. (I apologise for these digressions, but the subject is complex and does not admit of a simple straightforward narration without loss of clarity). The special theory is based on two postulates — the postulate of the relativity of uniform motion and the postulate of the independence of the velocity of light on motion of its source. Its purpose was to reconcile the theories of kinematics and electromagnetism - which, in their existing form, were respectively relativistic and non-relativistic - and it purported to do so by so modifying the former so as to make it capable of imposing its relativistic character, which the modification did not remove, on the latter. But such an achievement clearly called for generalisation. Kinematics was only the part of general mechanics that covered uniform motions: the next step would naturally be to reconcile the two departments of physics for all motions. The direct course to this end would be, first, to derive transformation equations for relatively accelerated systems of co-ordinates — corresponding to the Lorentz transformation equations for systems in uniform relative motion — and then to express the equations of electromagnetism in a form invariant to these new transformation equations. This Einstein never attempted - or at least he published nothing along these lines, nor has anyone else - but what he did in his so-called general relativity theory was to generalise the relativity postulate alone, and then construct a law of motion of bodies that included their motions under their mutual gravitational influence, and held good for all systems of co-ordinates, in accelerated as well as uniform motions.

It was a great achievement, but it had the serious disadvantage of destroying the possibility of preserving the reconciliation with electromagnetism, which the special theory had claimed for uniform motions. The generalisation of the relativity postulate had the consequence that the other postulate — that of the constancy of the velocity of light, as it is generally called - could no longer be maintained. 'It will also be obvious,' wrote Einstein at the beginning of his 1916 paper, 'that the principle of the constancy of the velocity of light in vacuo must be modified.' Einstein's chief aim during the remainder of his life was to construct 'a unified field theory', i.e. a theory in which his general relativity theory of mechanics was reconciled with electromagnetism, but he did not succeed. What is usually called 'the general theory of relativity' is thus not, in the full sense, a generalisation of 'the special theory of relativity'. If the criticism of the special theory here advanced — which seems to me unanswerable, and certainly has not been answered — is sound, a possible explanation of Einstein's failure is that he was attempting the impossible, but that does not mean that the 'general' theory is necessarily wrong. The failure of the special theory may lie in the falsity of the postulate of the constancy of the velocity of light and not the postulate of relativity, in which case a theory based on a generalisation of the latter alone may still be valid. The matter, however, is not important for our present purpose, except insofar as it does give some support - very far indeed from proof - for the view that the error in the special theory does lie in the postulate of constant light velocity, for Einstein's theory of gravitation does have some support — again very far from proof — from observation, and nothing is so far known fatally at variance with it.

As if this were not enough, there was the additional complication resulting from the name of the theory. The 'relativity' theory was ascribed to Lorentz, Einstein and Minkowski as though these all contributed to the same set of ideas. The facts that Lorentz's theory was impossible without an ether and Einstein's impossible with one, that Lorentz and Einstein never thought of time as relating to anything but instants and durations while Minkowski never thought of it as relating to anything but 'eternity', that the basic idea of Minkowski was 'space-eternity', which meant nothing whatever in the original papers of either Lorentz or Einstein - all these differences were completely obscured by their unholy alliance under the one word 'relativity'. Phrases like 'time-dilation', which meant nothing to anybody, were freely used to describe 'Einstein's special relativity theory', and 'time' and 'space' were declared to be interchangeable ('one man's space is another man's time', as Jeans put it), so that even those who took the trouble to look up Einstein's 1905 paper and found there nothing to which they could possibly attach such notions, became convinced that what normally they would have understood without any difficulty at all must contain some mysterious essence which they were incapable of apprehending, The net result was that they gave up the attempt to understand the matter and submitted to the uncritical acceptance of 'Einstein's special relativity theory' with resignation. That state has persisted ever since, with increasing irresponsibility of the 'mathematicians', freed now from the task of having to justify their pronouncements, however extravagant, and increasing mental inertia on the part of the 'experimenters', until the present state is reached in which so simple a question as that which I have put has remained unanswered for 13 years and no one is in the least disturbed about it.

That the state of mind which I have described is that which actually existed among physicists in 1919 and the years immediately following I know from my own experience, but it can be amply verified from the records. I was, of course, a mere onlooker, but a specially privileged one, for at the Imperial College, where I was successively a demonstrator and lecturer in physics during this period, I was in close association with the two men - one a mathematician and philosopher and the other a leading experimental physicist and astronomer — through whom, perhaps better than any others, it was possible to observe and sense the general intellectual climate of the time. They were Professor A. N. Whitehead and Professor A. Fowler. The former, as is well known, had his own original ideas on relativity, while Fowler, in whose department I worked and to whom I acted as a sort of unofficial private secretary, was at that time President of the Royal Astronomical Society and General Secretary of the newly-formed International Astronomical Union, besides being the acknowledged leader in spectroscopy which was the foremost experimental activity in physics at that time. Thus I had exceptional opportunities of meeting, in both public and private gatherings, the outstanding visiting astronomers and physicists of the time and discussing with them relativity and other problems. Further, I was frequently in contact with Sir Richard Gregory, the editor of Nature, who had been a fellow-student of Fowler's, and he used me for reviewing and other purposes connected with the journal, so that I was enabled to see various communications of interest and importance from those best qualified (and, incidentally, many from those not qualified at all) to write on relativity. There could hardly have been a more favourable situation for observing the general effect of the relativity theory on scientists. It was as I have described it.

Examples of the persistence of this confusion during the succeeding years could be given galore, but I restrict myself to one. Even as late as 1942, no less an authority than Professor P. S. Epstein of California, who was active in the field at the time of origin of the theory, could quote,¹⁶ in support of his contention that on Einstein's theory the 'relativity contraction' was 'real', Lorentz's statement made in 1927: 'I should like to emphasize the fact that the variations of length caused by a translation are real phenomena, no less than, for instance, the variations that are produced by changes of temperature'. What he made of Eddington's statement that 'nothing whatever happens to the rod', I do not know.

Epstein was writing as a mathematical physicist, and even he failed to see the essential distinction between the theories of Lorentz and Einstein. The plight of the experimental physicists may be imagined. I have quoted Whitehead to the effect that they were panic-stricken by the necessity of studying the theory of tensors. In fact they did not study it, but left it to the mathematicians. However, this was relatively unimportant because tensor theory, though essential for the general relativity theory, could be avoided when one was dealing only with the special theory, and it was only the latter that physicists in general were compelled to deal with. They could leave gravitation to the mathematicians, but they could not leave electromagnetism; that was essential, everyday physics, and they had to teach it and conduct their researches in terms of its theoretical requirements. Apart from a few like Rutherford, who ignored the whole thing and went on with his experiments, they took the only course available in the circumstances. Naturally they could not make sense of the confusions which I have described, but they could use the equations of the Lorentz transformation and apply them as a 'relativity correction' (blessed phrase) to the requirements of the Maxwell-Lorentz theory. To justify this to their students they learned the appropriate phrases from the 'experts' and escaped awkward physical questions by jumping freely between Einstein and Lorentz (they were both 'relativity', of course) according to the needs of the moment. The equations worked, so the 'experimenters' became convinced that the theory, whatever it was, must be right. The superior minds acknowledged that they did not understand it, but the majority could not rise to that height. Nothing is more powerful in producing the illusion that one understands something that one does not, than constant repetition of the words used to express it, and the lesser minds deceived themselves by supposing that terms like 'dilation of time' had a self-evident meaning, and regarded with contempt those stupid enough to imagine that they required explanation. Anyone who cares to examine the literature from 1920 to the present day, even if he has not had personal experience of the development, can see the gradual growth of dogmatic acceptance of the theory and contempt for its critics, right up to the extreme form exhibited today by those who learnt it from those who learnt it from those who failed to understand it at the beginning. They are not worth quoting; the candid admissions I have cited in Part One from the mature leaders in the subject are sufficient evidence of the present state.

It is easier to be wise after the event than before it. The impossibility of special relativity - so obvious now, when one looks at my simple question and realises its clear unanswerability — was by no means obvious then: incredible as it may seem, this nevertheless was so. I certainly had no suspicion of the obvious truth, but believed the theory to be a landmark in the history of physical thought - and, I may add, I still think that Einstein's perception of a possible escape from the dilemma of the time a mark of the highest genius, though his failure to see that it could not be actual when it needed such slight additional thought to make that unmistakably evident, reveals all too clearly the limitations of that genius. But the transformation that the theory had wrought in the attitude of physicists to their researches - a transformation so ominous for the future, especially at a time when the political situation on the Continent was revealing the displacement of reason by dogmas concerning race rather than mathematical fancies — seemed, nearly 40 years ago, so plainly apparent that I could not understand why physicists in general were so blind to it. With the encouragement of Sir Richard Gregory I wrote an article entitled 'Physics and the Public Mind' which he published in Nature of 2 June 1934 and in which I attempted to check the bartering by physicists of intelligent thought for blind acceptance of absurd interpretations of unintelligible mathematics. Thinking it at that time to be a calamitous effect of what in itself was a great advance in human thought, I began with a quotation from Browning:

This evoked much approval from thinkers of all types except those who, in this connection, alone mattered — the physicists themselves, who gave it no attention whatever. Now that the 'few decades' have passed I hope its universal importance may be recognised and acted upon by physicists before those whose interests are now so dependent on their activities are moved, by the course of events, forcibly to restrict those activities. However, at that time the ineffectiveness of that effort led to a second article entitled 'Modern Aristotelianism' - again with the approval of Gregory, who published it in Nature of 8 May 1937 and followed it by a special Supplement on 12 June 1937 containing comments from various writers (I have already quoted a passage from this discussion in connection with Synge's illuminating illustration of it concerning my supposed 'hoax'). I concluded this Supplement with the following paragraph:

So much for the past; now let us return to the present. The next step must be the determination of which of Einstein's two postulates is wrong, for if they are both granted the theory follows by logical necessity. That is a question needing an experimental answer and speculations in advance of experiment are of little profit. I should prefer not to make them, but the impossibility so far of persuading anyone of the need for experiment (why test a theory that you know cannot be wrong?) justifies an attempt to discuss the various possibilities, and this I shall attempt briefly to undertake. Before doing so, however, the occasion calls for some comments on the most famous problem in the criticism of special relativity, which has constantly arisen throughout its history - the so-called 'clock paradox' Qr 'twin paradox'. It has been a common and very effective device in this field to avoid the necessity of admitting a contradiction by calling it a 'paradox': it is thereupon automatically regarded by those who do not consider themselves experts in the subject as something to which there is of course an answer, like the paradox of Achilles and the tortoise, which it is not their concern to provide and to which therefore they need pay no further attention). Although the importance of this problem vanishes if the inadmissibility of the special relativity theory is admitted, it deserves attention for historical reasons, and I shall therefore give it that attention in the following chapter.